Использование методов Крамера, Жордано-Гаусса при построении матриц через алгебраические дополнения

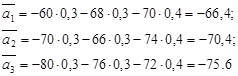
и

.

б) Оптимальной по критерию Лапласа будет чистая стратегия , т.к. именно при ней средний выигрыш

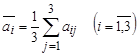
достигает максимального значения:

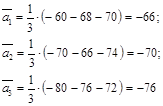
И .

в) Оптимальной по критерию Вальда будет чистая стратегия , т.к. именно при ней наименьший выигрыш статистика будет максимальным (см. таблицу 5).

.

г) Чтобы воспользоваться критерием Сэвиджа, составим матрицу рисков с элементами

(таблица 6)

Таблица 6

Так,

и т.д.

Оптимальной по критерию Сэвиджа будет чистая стратегия , т.к. именно при ней максимальный риск будет минимальным (см. таблицу 6)

.

д) Оптимальной по критерию Гурвица будет чистая стратегия , т.к. именно при ней величина