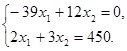Использование методов Крамера, Жордано-Гаусса при построении матриц через алгебраические дополнения

Для определения точки, в которой целевая функция принимает наибольшее значение, перемещаем линию уровня в направлении вектора-градиента до тех пор, пока она займет крайнее положение в области допустимых значений. Для данной задачи это точка А с координатами (0; 150). В этой точке значение целевой функции -

.

Итак, максимальная прибыль составляет 1500 руб. и достигается при реализации 150 кг продукциитоварной группы вида .

Определим максимальный объем выпуска при ограниченных ресурсах. Для этого решим графически задачу

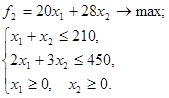
Координаты вектора-градиента . Максимальное значение целевой функции достигается в точке В (см. рисунок 1).

Координаты точки В определяем из решения системы, составленной из уравнений прямых, пересекающихся в этой точке:

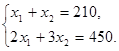
Решая систему, находим

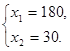
Следовательно, точка В имеет координаты (180; 30). В этой точке значение целевой функции

.

Итак, стоимость реализованных товаров составляет 4440 кг и достигается при реализации 180 кг продукции товарной группы вида и 30 кг продукции товарной группы вида.

Отрезок АВ является областью компромиссов.

Запишем относительные отклонения для обеих функций:

,

.

Для построения дополнительного ограничения замещающей задачи приравняем отклонения , т.е.

После упрощения этого выражения получим

Замещающая задача в соответствии с методом равных наименьших относительных отклонений будет иметь вид

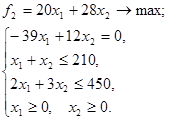
Рисунок 2

цена продукция прибыль

Областью допустимых значений замещающей задачи является отрезок OD (см. рисунок2). Максимальное значение целевой функции достигается в точке D. Координаты точки D определяем из решения системы, составленной из уравнений прямых, пересекающихся в этой точке: